Critical Relationship between Respiratory Rate, Heart Rate and Cadence
In the newer models (Forerunner 945, Fenix 6, MARQ, Vivoactive 4, etc.), with the heart rate band, you can further detect your breathing rate (only for some of the models), and can also continue keeping a record throughout the day everyday.
This value serves the same purpose as the heart rate. It can help us monitor the intensity in a timely manner when exercising. Next, we’ll be looking at how to apply the respiration rate in exercise.
What is Respiration Rate
One complete breath includes both inhalation and exhalation. The respiration rate is defined as the number of breaths completed per minute.
Normally, the number of breaths of an adult per minute is around12-20 times; however, this refers to the non-exercise state. When exercising, the number of breaths is bound to be higher than the interval of 12-20.
Consider the difference in respiration rate between the exercise period and the non-exercise period. We will be discussing the two types, exercise period and non-exercise period, separately below.
Part I: Respiration Rate and Heart Rate (Exercise Period and Non-Exercise Period)
[Exercise Period]
The following table is the three exercise types that I have recently done: Strength, Run, and Elliptical. I recorded my minimum, maximum, average heart rate and respiration during the exercise period. I also calculated the ratio of heart rate ÷ respiration rate.
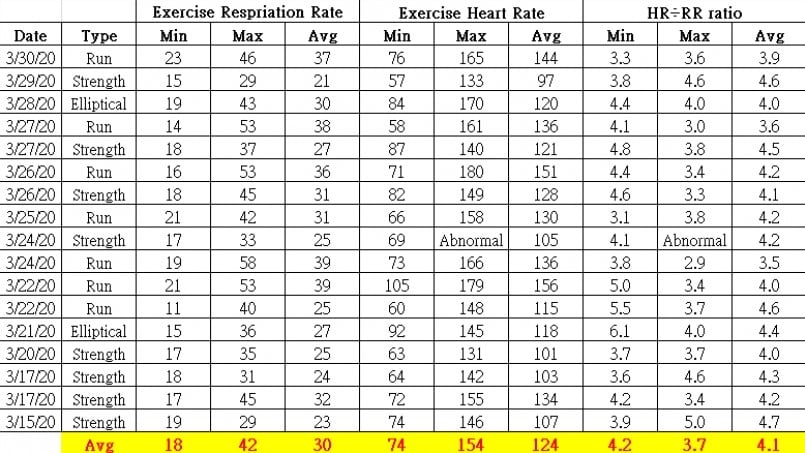
After taking the average of the 17 collected data, we discovered that the ratio of heart rate ÷ respiration rate is about 4 regardless of whether it is average, minimum, or maximum.
This magical number is really close to the information available on the Internet. The average adult’s respiration rate to heart rate ratio is approximately 1:4, which means that for each breath, the heart beats 4 times.
The interesting thing is that the ratio of respiration rate to heart rate mentioned in this document is the ratio obtained during the “non-exercise period,”. However it was unexpected that the ratio measured during the exercise period was actually so in line with that.
Note: I used the HRM-Tri heart rate band + FR945 to carry out the testing for the above information.
Although from the overall average, the data is very consistent with the principle of respiration rate : heart rate = 1:4. If we analyze the changes during the actual running process, will we get the same result?
The following graph shows the data on the relationship between respiration rate and heart rate for my 3/26 run (Tempo Run):
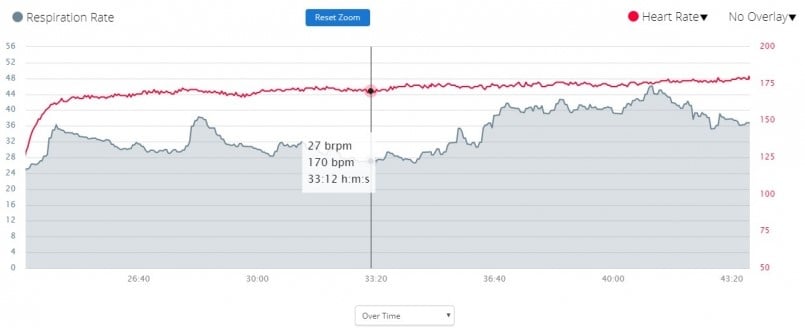
From the graph, we can see that the average heart rate of exercise at 20 minutes 30 seconds is around 171 bpm (pace 3’53’/k), and the average respiration rate is 36brpm.
Hence, the heart rate ÷ respiration rate = 4.75, which is higher than the average value of 4.2 during this run. This is mainly because when at a faster pace, the heart rate is comparatively higher, yet the respiration rate does not need to increase as much.
Respiration Rate : Heart Rate = 1: 4 is the overall average concept.
However this may not be the case in extreme situations.
For example, through my observation, I saw that my maximum respiration rate was about 58 ~ 59, and my maximum heart rate reached 188, so the conversion ratio was about 3.2.
When I’m sleeping, my minimum heart rate was 40 and my minimum respiration rate was 6, so the conversion ratio was about 6.67. That is to say, although the overall ratio is still around 4, but from the lowest at 3.2 to the highest at 6.67 still may occur.
[Non-Exercise Period]
The function I use during the non-exercise period is the watch’s Garmin Elevate to detect my respiration rate throughout the day. For the non-exercise period, the respiration rate is subdivided into two types: average when awake and average when asleep.
Although the watch also has the function to provide the 24-hr heart rate, it only provides the trend chart and does not calculate the average heart rate for the day. Also, if I exercised that day, then the heart rate throughout the day will also include the exercise heart rate.
Therefore I chose the “Sleep Heart Rate” as the reference for the minimum, maximum, and average heart rate during the non-exercise period. For the minimum and maximum values of the respiration rate during the non-exercise period, I also used the minimum and maximum values measured during sleep.
In the calculation of heart rate ÷ respiration rate ratio, the data used are the ones collected during sleep. The average respiration rate when awake is used only as a reference.
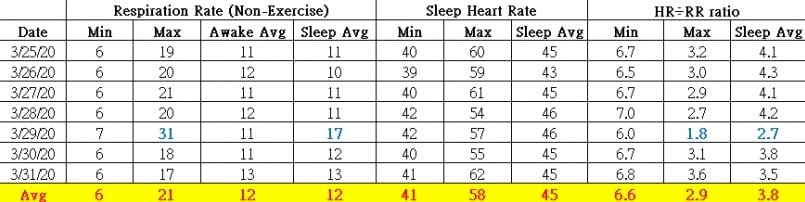
The data was collected for 7 days from 3/25 to 3/31 for this experiment.
We’re able to see that there’s quite a big difference between the ratio calculated from both the “minimum” and “maximum,” which were, respectively, 6.6 and 2.9, and the value [4]. We speculate that the main reason is because both of these are peak values. They are the extreme outliers which occur during sleep, so they will cause a larger deviation in the calculated ratio.
However, if we take the average respiration rate and heart rate of the entire sleep data, the calculated ratio of 3.8 is pretty consistent with the value of [4].
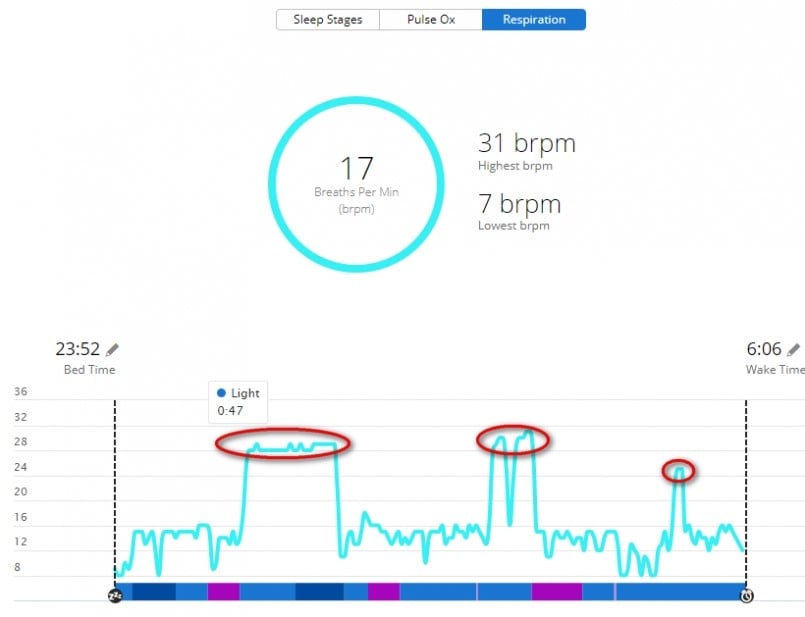
The data of the maximum respiration rate and the sleep average respiration rate for 3/29 in the table are shown in blue, mainly because the data for that day are abnormal.
It can be inferred that the reading may have been affected due to the body pressing on your hand during sleep. From the graph below, we’re able to see that the value of the respiration rate during sleep for that day was abnormal:
Through Garmin Connect, we can view the trend graph of the respiration rate throughout the day. However this is only for the “non-exercise period”. See the figure below.
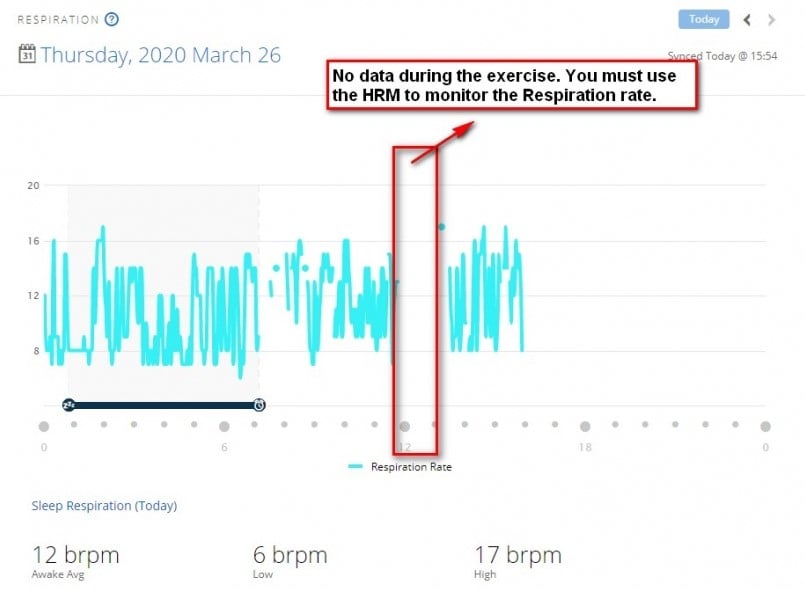
You can use the 24-hr respiration rate function to check the respiration rate at each point in time, and it will display the three values, namely the average, the minimum, and the maximum, for the period being awake.
If you need to view the average during sleep, you must enter from the sleep analysis graph to view it.
The respiration rate was not recorded between 12 o’clock and 1 o’clock (did running exercise), because the watch uses HRV to analyze. If you are overly excited, the Garmin Elevate will not be able to make the detection.
If there is a need to look at the respiration rate when exercising, do wear a heart rate band * with a compatible device * for it to be recorded. The said exercise mode needs to be selected in order to view it.
*HRM-Tri + Forerunner 945
Part II: The Frequency of Strides and Respiration Rate When Running (Only During Exercise)


In Garmin Connect (GC), there are instructions for how to breathe when running. You’ll find that different frequency of strides and breathing methods are adopted according to different speed requirements, such as the common 2 to 2, which is inhale while taking two strides and exhale while taking two strides.
Of course, in actual running, you just need to breathe smoothly and naturally. You don’t have to deliberately do 2 inhale-2 exhale or 3 inhale-3 exhale, but since Garmin ’s equipment can now detect the respiration rate, it is also quite interesting to analyze [afterwards] and understand your own breathing pattern when running.
The following is an analysis of my recent running data:

Pacing speed will affect stride and breathing. Hence we listed the “pacing” column as one of the reference indicators.
It does not matter whether the pace is fast or slow. On average, one breath cycle is completed for every 4.3 to 5.4 steps, so the difference is not large.
Comparing to the instructions provided by GC, this is somewhere between the modes of 3 to 3 and 2 to 2, that is, one breath cycle is completed every 4 to 6 steps.
Note: The minimum and maximum values in the table are for reference. These two values are regarded as peak values.
[Conclusion]
Do you now understand your own respiration rate? And the number of steps you can run for each breath cycle? Now you know that the respiration rate : heart rate ratio is about 1:4. Knowing these do not substantially help improve your own running ability.
To run better, faster, and with more power, years of running practice are still required.
However, after observing and comparing for a long period of time, you may be able to find out early whether your body has abnormalities.




